Index
Calculation of the electron radius under the conditions of the Stern – Gerlach experiment
Calculation of linear rotational speed
Calculating the turning radius
Calculating the radius of the element
Calculating the number of elements
Calculation for Coupling Constant and Strong Interaction
Kinetic energy of the electron under the conditions of the Stern-Gerlach experiment
Calculation of the electron radius under the conditions of the Stern – Gerlach experiment
According to the hypothesis, the rotation of all the elements causes a magnetic moment (μE) equal to that produced by a circular and closed spiral of radius (R) traveled by an electrical intensity (I)
The equation for calculating the magnetic moment of a circular spiral is
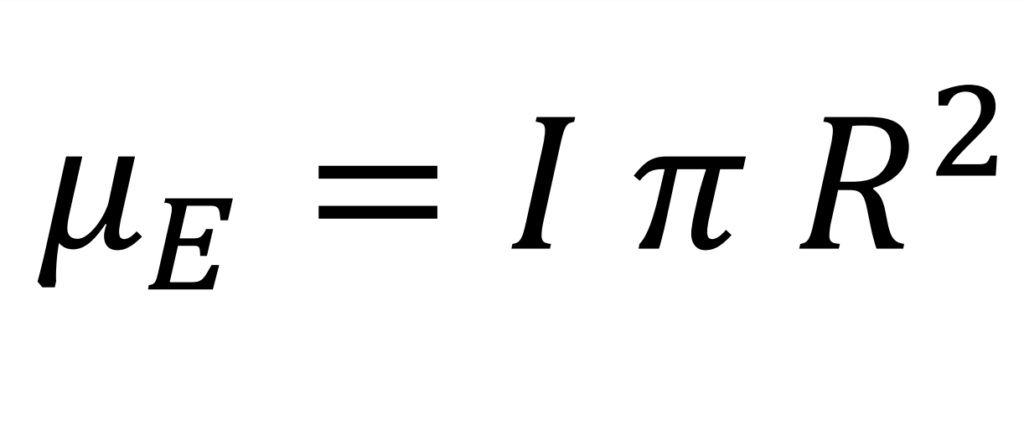
The resulting intensity is the quotient between the electric charge of the electron and the time taken to complete one revolution
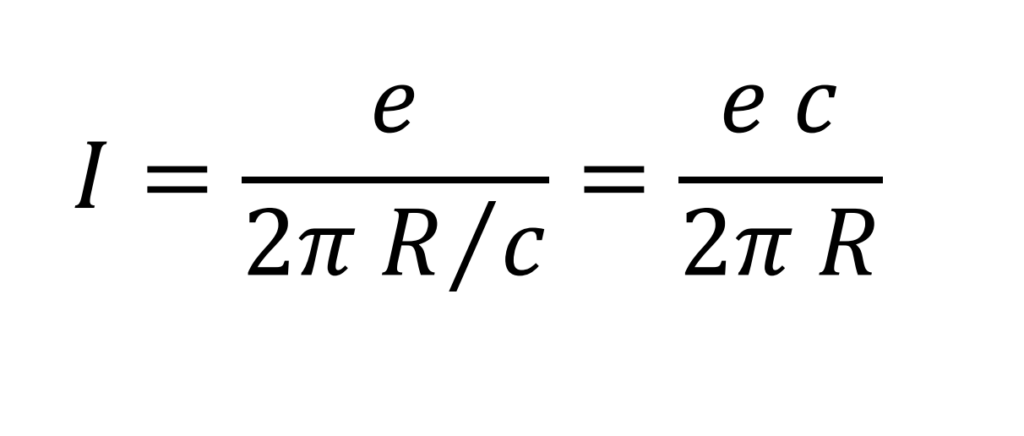
The expression for the magnetic moment
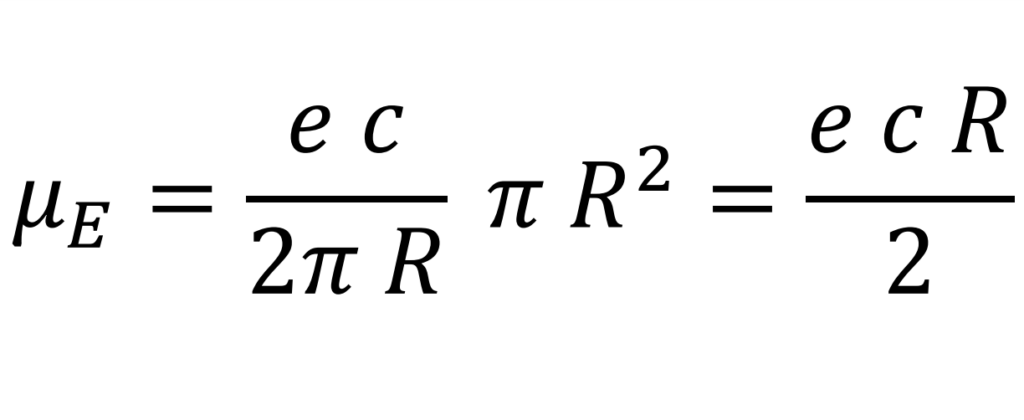
The electron radius

Calculation of the critical radius of the electron under the conditions of natural neutron formation in protostars
To initiate the transfer of electric charge and kinetic energy from the orbital electron to the central proton, the binding energy of any element minus its electrical potential energy must be equal to zero.
General expression for binding energy in strong interaction (Francisco Ynduráin. Electrones, neutrinos y quarks. La Física de partículas en el siglo XXI 2ª edición CRÍTICA 10.6 p145).
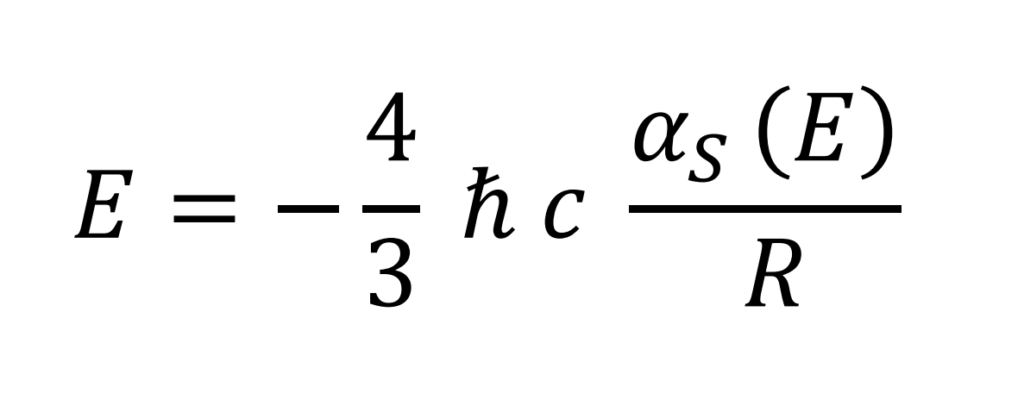
Binding energy per element (R is the radius of the electron and n is the number of elements)
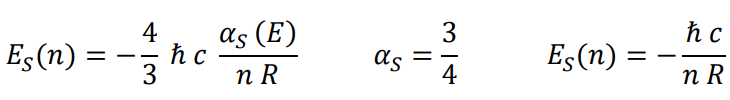
Electrical potential energy per element (d is the distance between the electron and the proton’s charge center)
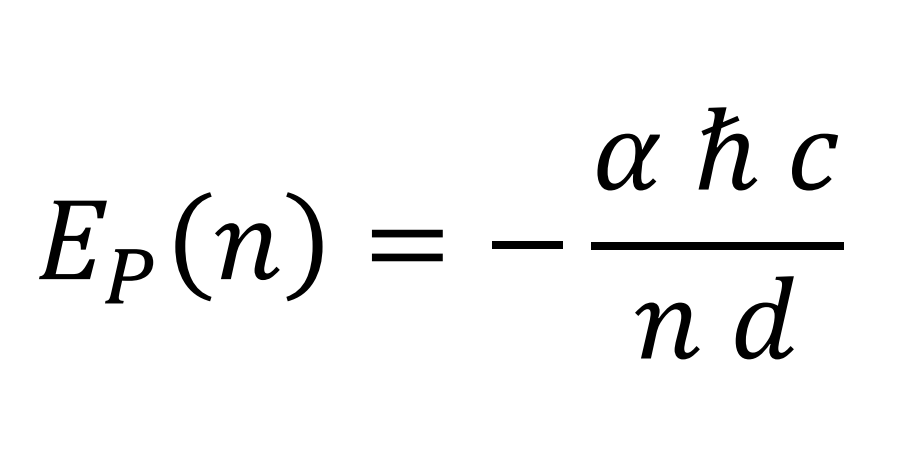
Equalizing the two expressions
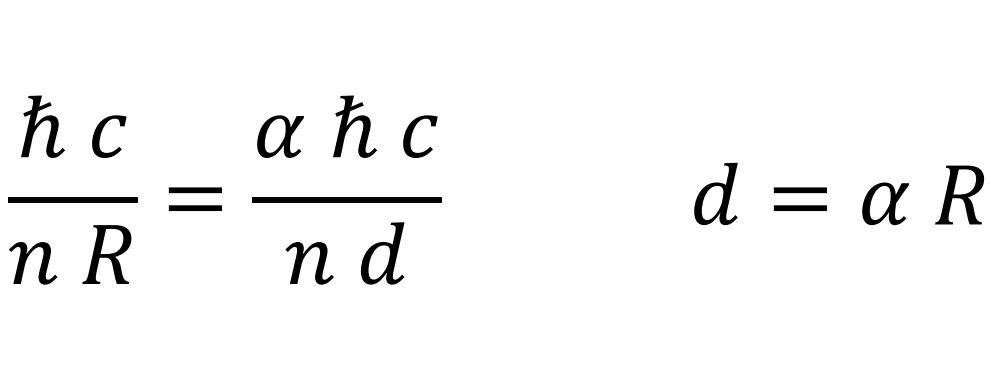
Distance between the electric charge centers of the proton and electron
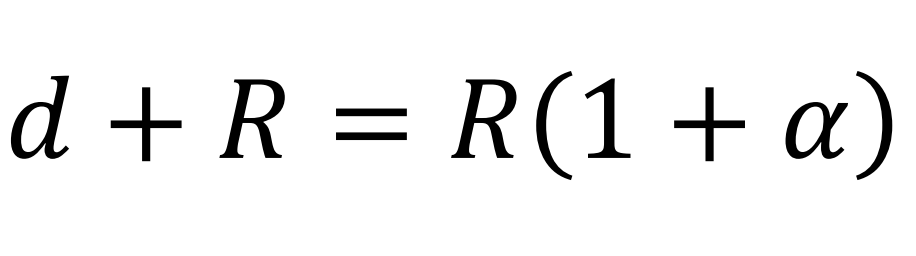
Volume occupied by the electron (cubic packing)
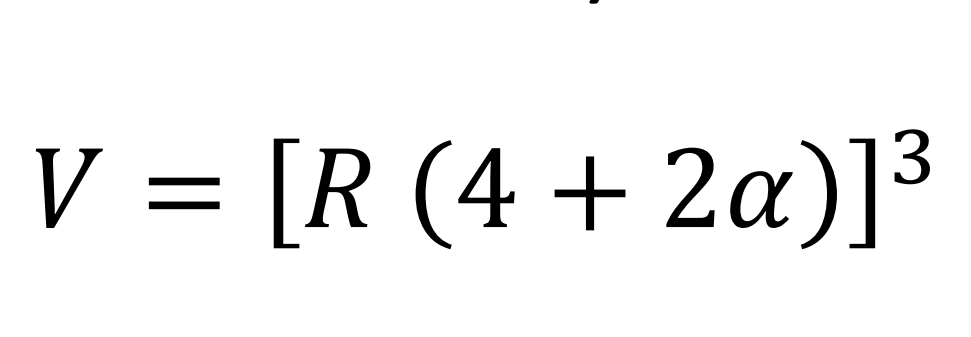
Volume occupied by the electron (spherical packing)
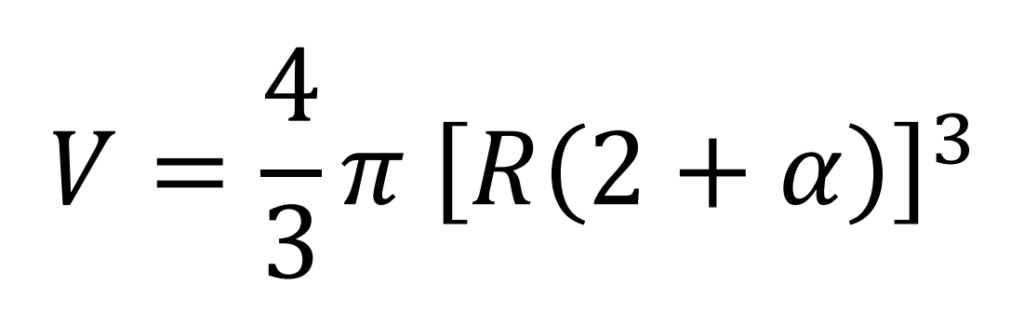
Empirical volume
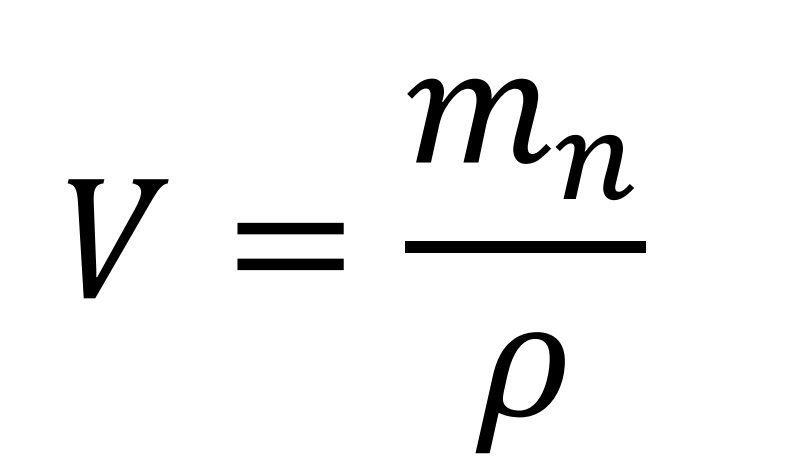
Clearing R (cubic packing)
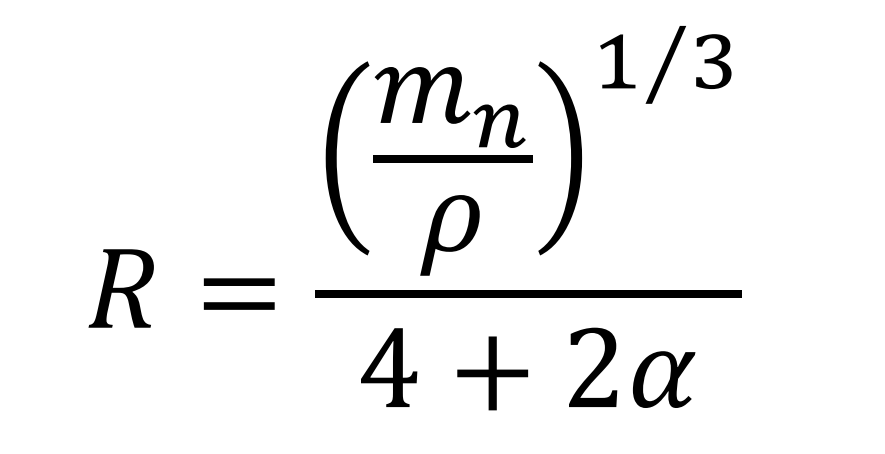
Clearing R (spherical packing)
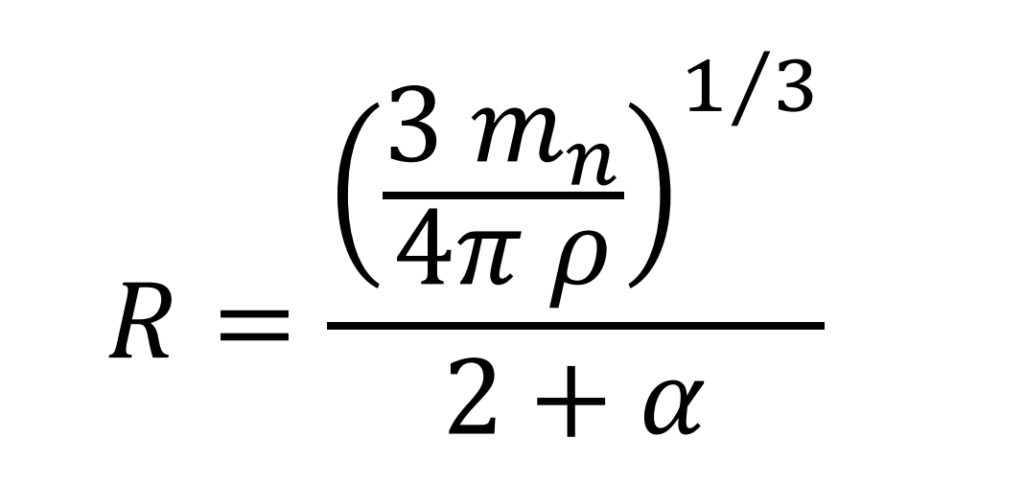
Electron radius (mean value)
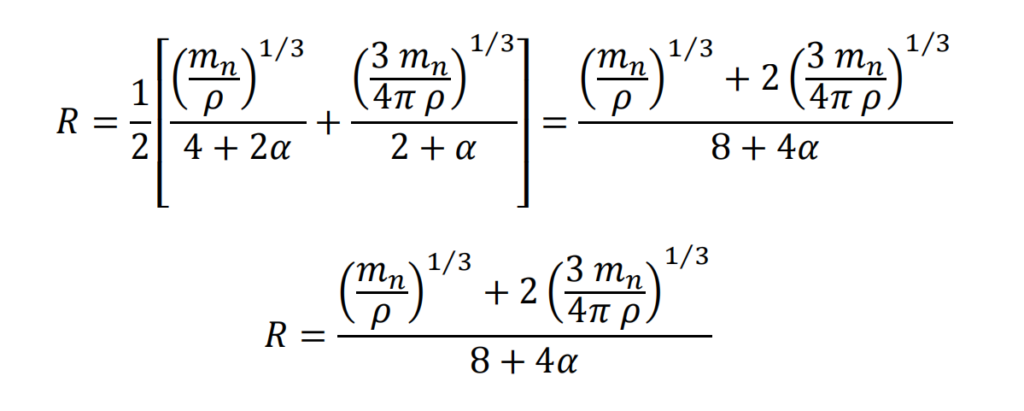
Calculation of linear rotational speed
The condition for achieving the stability of the element is that the sum of all the forces acting on any portion is zero. Lacking spin, the only forces at work are electromagnetic and gravitational.
The element is characterized by its radial symmetry. The centers of electric charge and mass coincide with the center of symmetry. Their values are e/n and m/n respectively, moving with a linear velocity v. The contribution of all the elements produces an effect similar to that of a direct, circular electric current.
Any portion of the element, with electric charge dq and mass dm, moves with velocity v perpendicularly crossing the magnetic field lines.
The Lorentz equation is applied, substituting the constants εo (electrical permittivity of the vacuum) and μo (magnetic permeability of the vacuum). Where e is the electric charge of the electron and n is the number of elements that compose it.
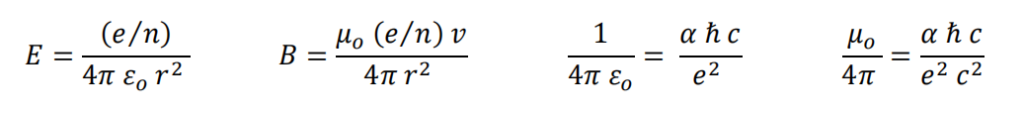
Electromagnetic interaction
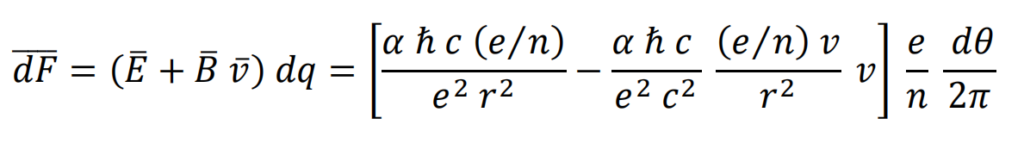
Gravitational interaction
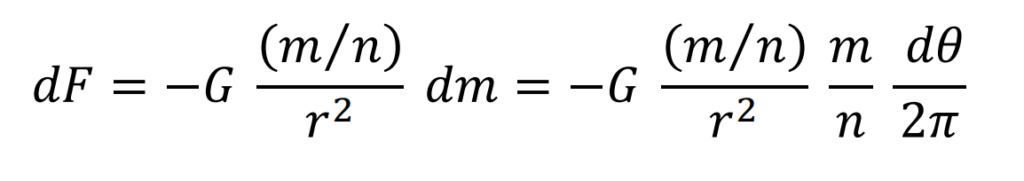
Sum of forces
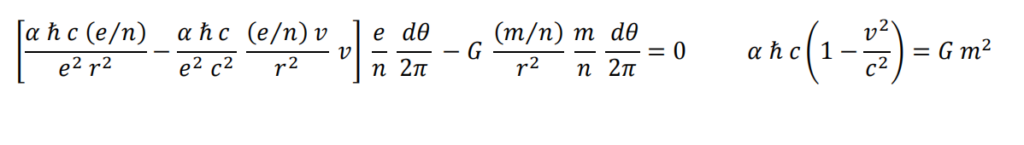
Clearing v

Expressing m as a function of mo

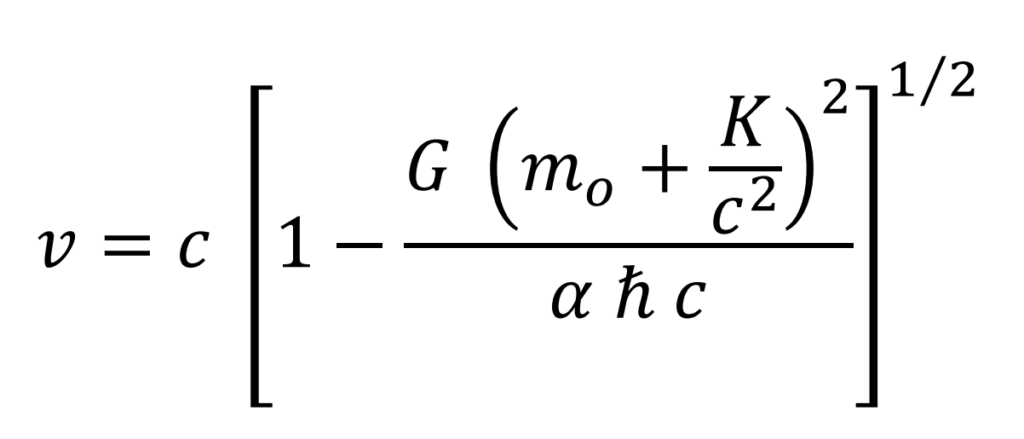
Calculating the turning radius
In 1924 Louis Victor de Broglie published his doctoral thesis entitled “Research on quantum theory” in which he formulated the hypothesis that a material particle is associated with a certain wave whose length is the quotient between Planck’s constant and linear momentum (Carlos Sánchez del Río. Física Cuántica 5ª edición Pirámide 3.3.11)
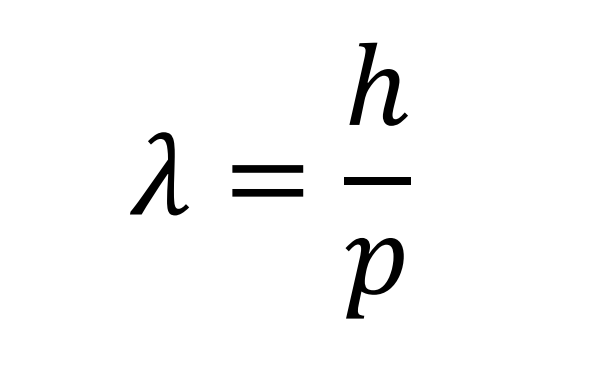
His hypothesis was experimentally validated in 1929, receiving the Nobel Prize in Physics.
The turning radius of the electron is considered equal to the value of its associated wavelength expressed in reduced form. In this way, the stationary wave condition is met and there are no radiation losses in the spinning motion. Situation similar to the electron orbit of the hydrogen atom for n = 1.
Carlos Sánchez del Río. Física Cuántica 5ª edición PIRÁMIDE 5.4.20
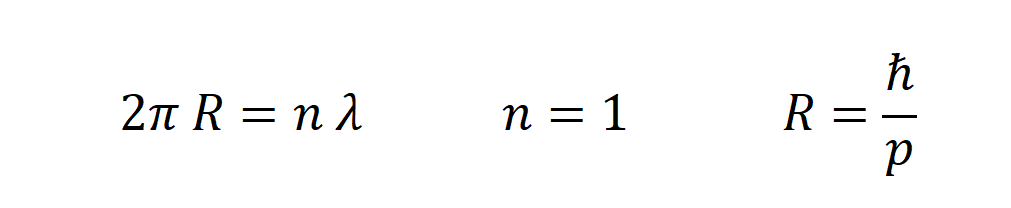
Linear momentum of rotation (for a very wide range of energy)
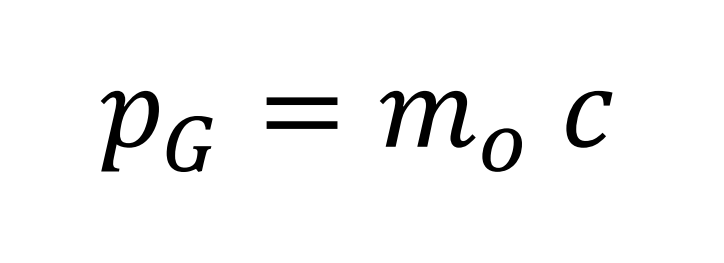
Linear momentum of translation (Carlos Sánchez del Río. Física Cuántica 5ª Edición PIRÁMIDE 2.4.15)
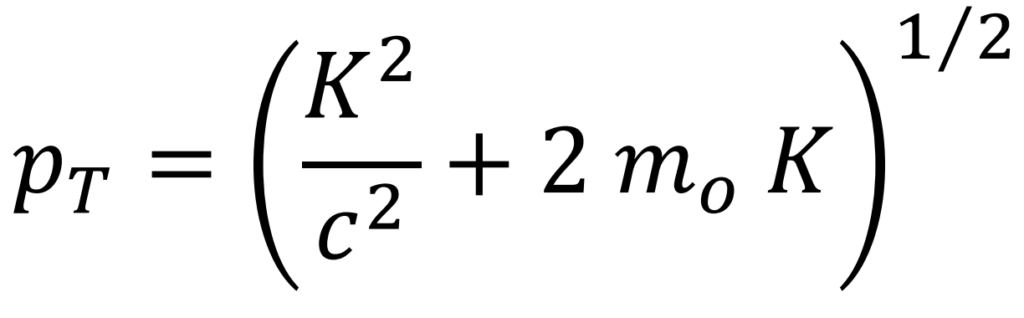
Expression for turning radius
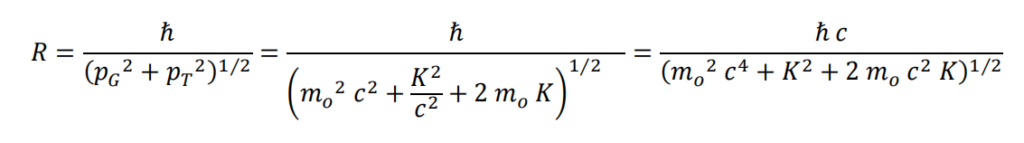
Simplifying
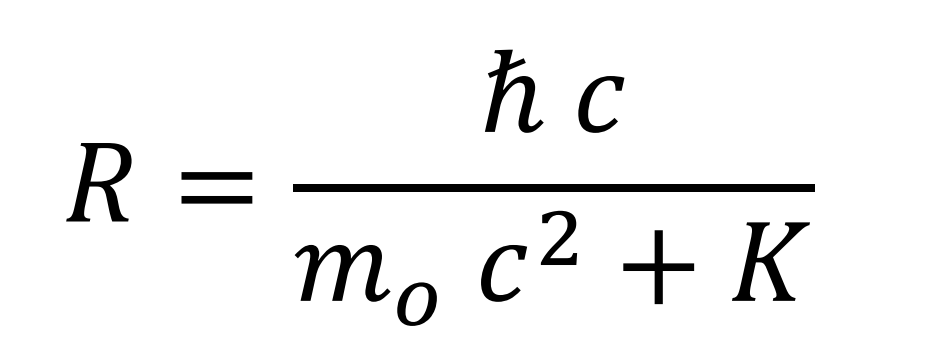
Calculating the radius of the element
The velocity v corresponds to the linear velocity of the center of symmetry of any element. The expression for the angular velocity will be
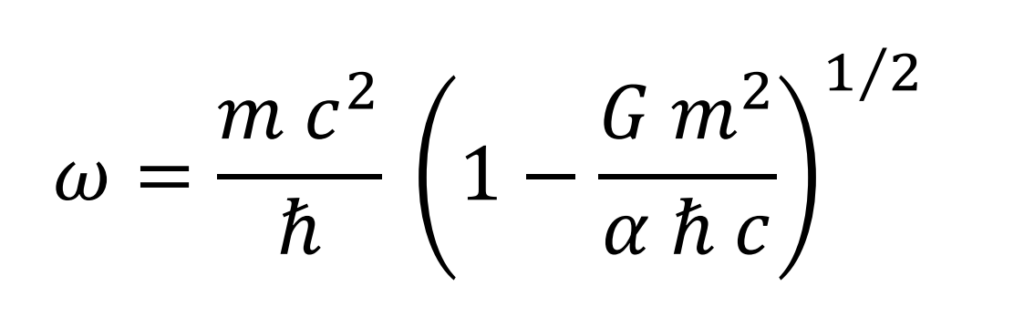
According to the theory of special relativity, the speed of propagation of light in the vacuum c is considered a limit that cannot be exceeded by any moving object.
Assuming that the element has radial symmetry with a radius r, the criterion applied to calculate it, will be that its peripheral velocity is infinitesimally less than c in the special case of the electron at rest. In this case the values of R and v are maximum and the mass is mo

Calculating the number of elements
The value of the fine structure constant α increases with the energy.
Francisco Ynduráin. Electrones, neutrinos y quarks. (La Física de partículas en el siglo XXI 2ª edición CRÍTICA 10.7 p149).
Values are assigned for the fine-structure constant, α0 = 1/137,036 and α91.2GeV = 1/128,96.
The mass of the electron as a function of its rotational speed is given by the expression

In the special case of a practically zero rotational speed, a value of 1 is hypothesized to the fine structure constant α. The expression for the mass of the electron coincides with the Planck mass.
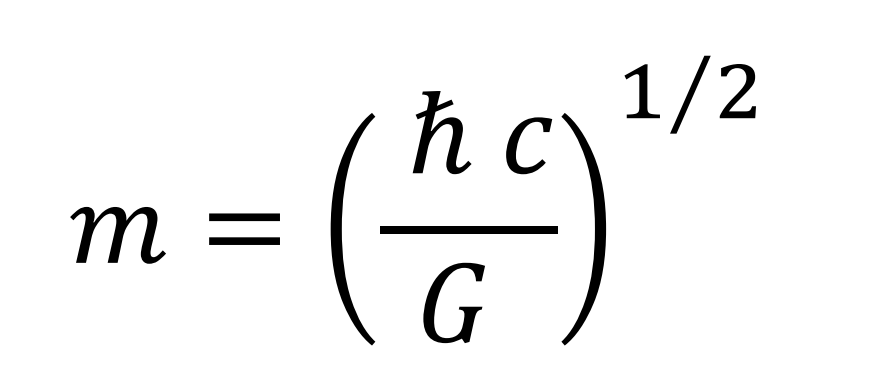
The value of the orbit radius for this case coincides with the Planck length.
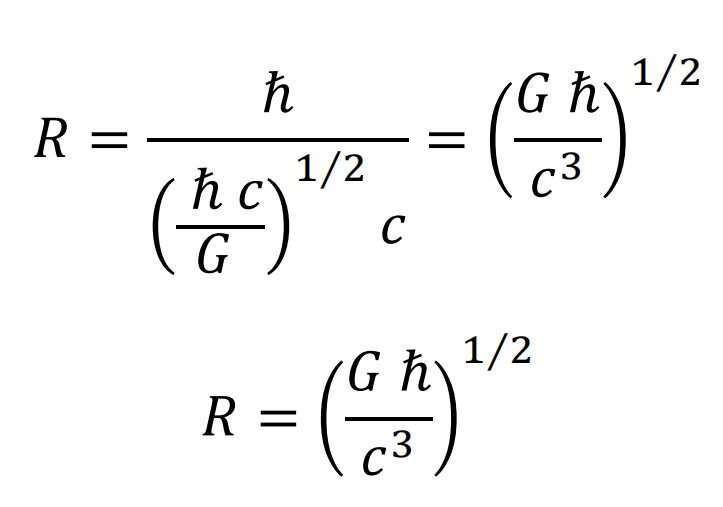
The elements would be grouped adjacent, occupying in their entirety the length of a circle of radius equal to the Planck length.
The number of elements is the quotient between the length of the orbit and the diameter of the element
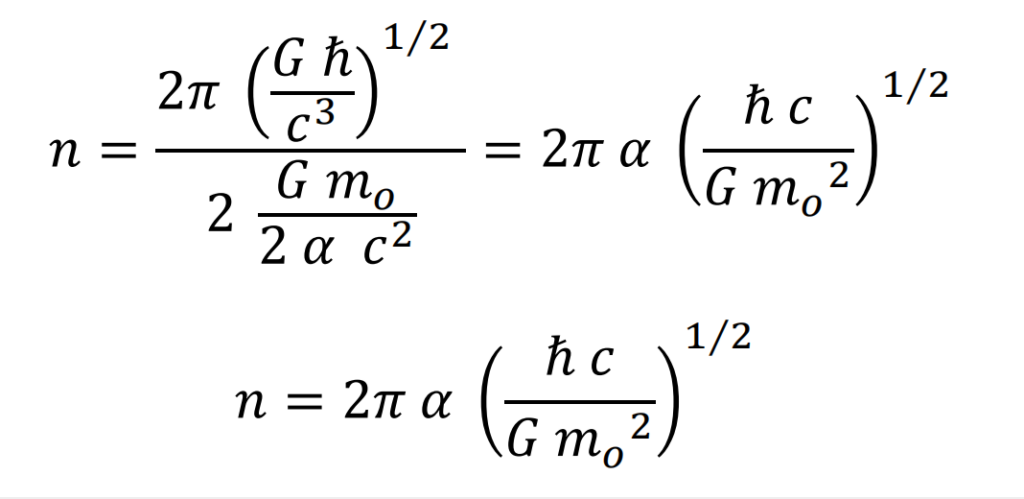
As a curiosity, the value of n calculated by the hypothesis coincides practically with a quarter of the product of Avogadro’s Number by the Fine Structure Constant
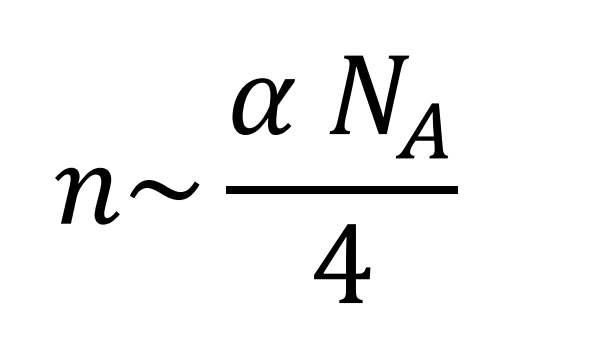
Calculation for Coupling Constant and expression for Strong Interaction
For the electron to be stable, the sum of all the forces acting on any element will be zero.
Inertial force
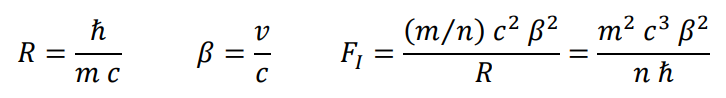
Electrical interaction
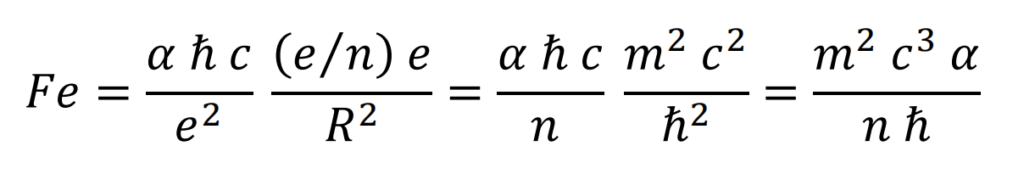
Gravitational force
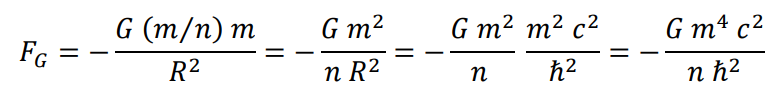
Sum of forces and expression of the new interaction
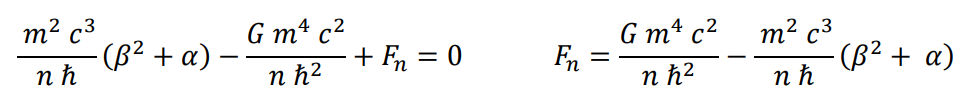
General expression for strong interaction (Francisco Ynduráin. Electrones, neutrinos y quarks. La Física de partículas en el siglo XXI 2ª edición CRÍTICA 10.6 p145).
Expression for strong binding energy
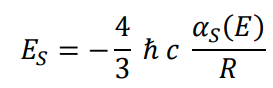
Equalizing the two expressions for interactions and substituting R
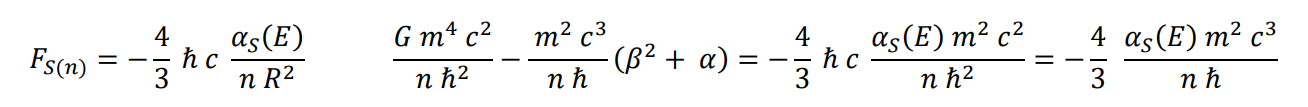
Clearing
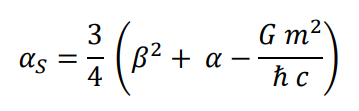
Expression for strong interaction, gravitational interaction is disregarded
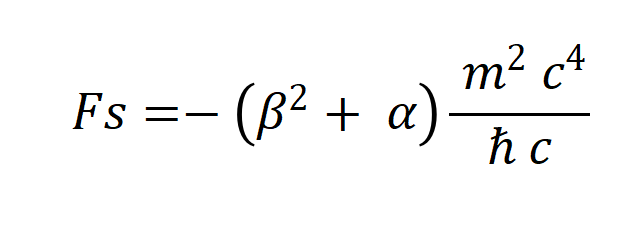
Kinetic energy of the electron under the conditions of the Stern-Gerlach experiment
The kinetic energy will be similar to the first ionization energy of the silver atom (Ag → Ag+).
E (Ag→Ag+) = 731 kJ/mol = 7,58 eV/atom
Rounding, K = 8 eV
Kinetic energy of the electron under the initial conditions of the neutron formation process in protostars
The kinetic energy corresponds to the product of the difference in the mass of the neutron minus the masses of the proton and electron at rest, multiplied by c2
Neutron mass multiplied by c2 939,565 MeV
Mass of the proton multiplied by c2 938,272 MeV
Mass of the electron at rest multiplied by c2 0,511 MeV
K = 939,565 – 938,272 – 0,511 = 0,782 MeV
In Bilbao on October 15, 2024.