GONZALO GONZALEZ BUSTINDUY

 

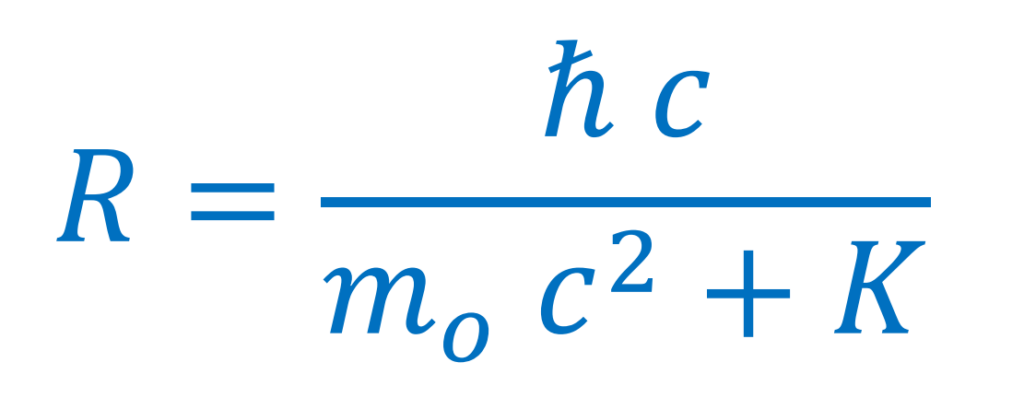
Hypothesis statement

 

The electron is considered to be composed of a number (n) of identical elements endowed with electric charge, mass, color charge and zero spin that symmetrically arranged describe a circular orbit of radius (R) with a linear speed of rotation (v) practically equal, but inferior, to that of the propagation of light in the vacuum (c). 

The electron can be displaced by the action of an electric field and acquire a certain kinetic energy (K). In this case, the elements would be moved along a helical trajectory.

 

Number of elements

 

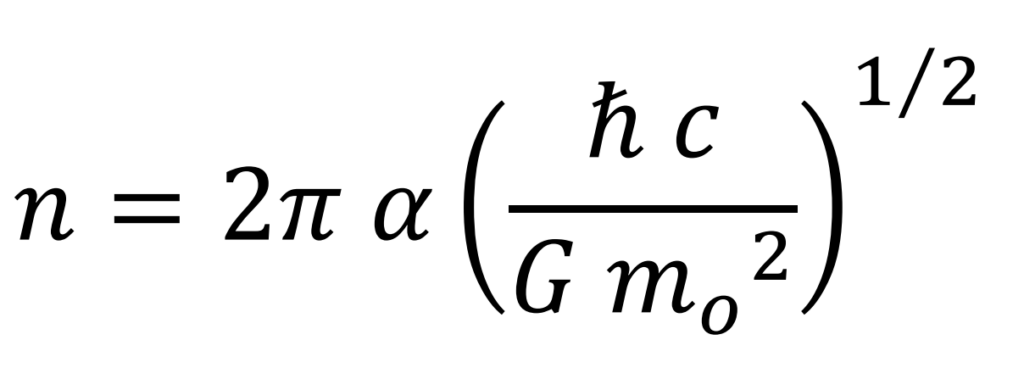
Radius

 

Linear rotational speed

 

 

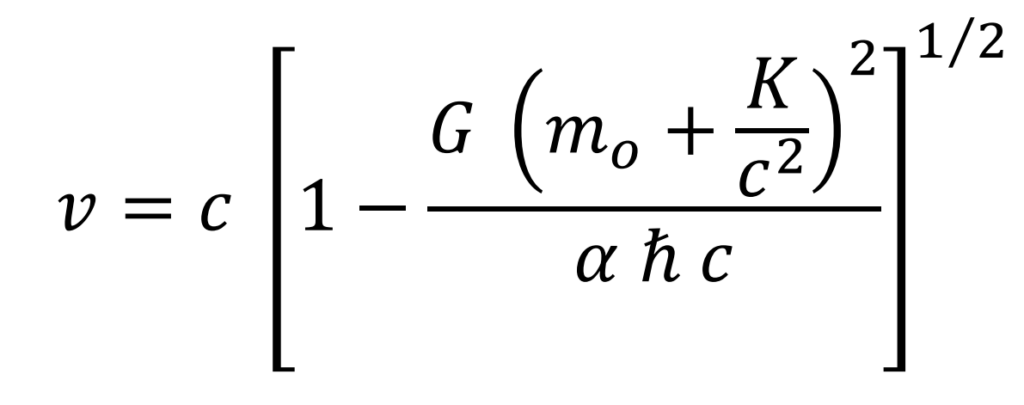
Image only illustrative of the orbit described by the elements of an electron.

 

Main objections to the hypothesis

 

Strong interaction non-existent.

There is no evidence of color charge in the electron.

 

Radiation and stability.

A system in orbit with an electric charge and speed close to the speed of light, would quickly lose energy due to electromagnetic radiation and would not maintain its stability over time.   

 

Value of the radius of the orbit.

It must be constant.

 

 

Rebuttal of objections

 

Strong interaction non-existent.

There is no evidence of color charge in the electron due to the low value of its resting mass, it is a lepton.

The intensity of the strong interaction is proportional to the square of the mass (see Mathematical Development, section Calculation for the Coupling Constant and Strong Interaction).

The intensity of the strong interaction for the electron is comparatively much lower, on the order of a million times, than that of a hadron (proton or neutron) and for this reason it goes unnoticed in most experiments, not being observed or detected.

 

Radiation and stability.

Indeed, if the wave associated with an electric charge in orbit is not stationary, it would quickly lose energy due to electromagnetic radiation.

The electron is stable because its associated wave is stationary (see Mathematical Development, section Calculating the turning radius).

 

Value of the radius of the orbit.

The wave can only be stationary if the value of the radius of the electron decreases with the increase of its kinetic energy, according to a certain expression (see Mathematical Development, section Calculating the turning radius).