Índice
Cálculo del radio del electrón en las condiciones del experimento de Stern – Gerlach
Cálculo de la velocidad lineal de giro
Cálculo del radio del elemento
Cálculo del número de elementos
Cálculo para la constante de acoplamiento y expresión para la interacción fuerte
Energía cinética del electrón en las condiciones del experimento de Stern – Gerlach
Cálculo del radio del electrón en las condiciones del experimento de Stern – Gerlach
De acuerdo con la hipótesis, la rotación de todos los elementos origina un momento magnético (μE) igual al producido por una espira circular y cerrada de radio (R) recorrida por una intensidad eléctrica (I)
La ecuación para el cálculo del momento magnético de una espira circular es
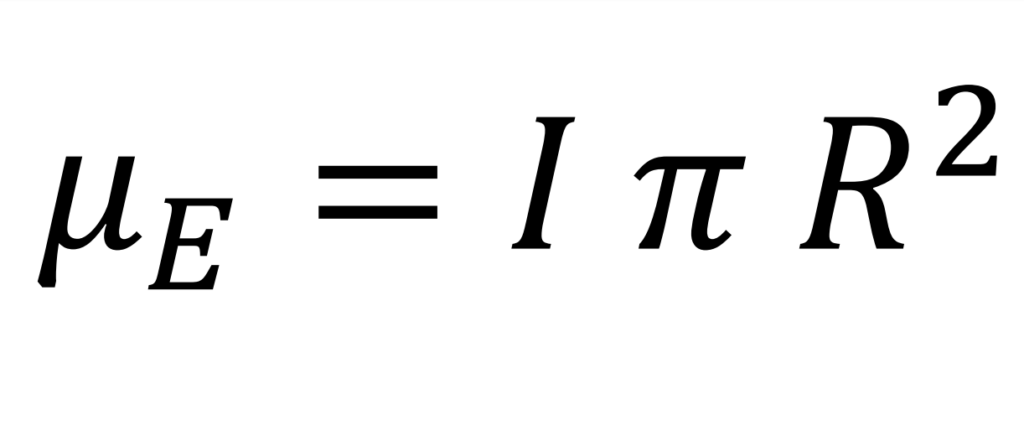
La intensidad resultante es el cociente entre la carga eléctrica del electrón y el tiempo empleado en completar una revolución
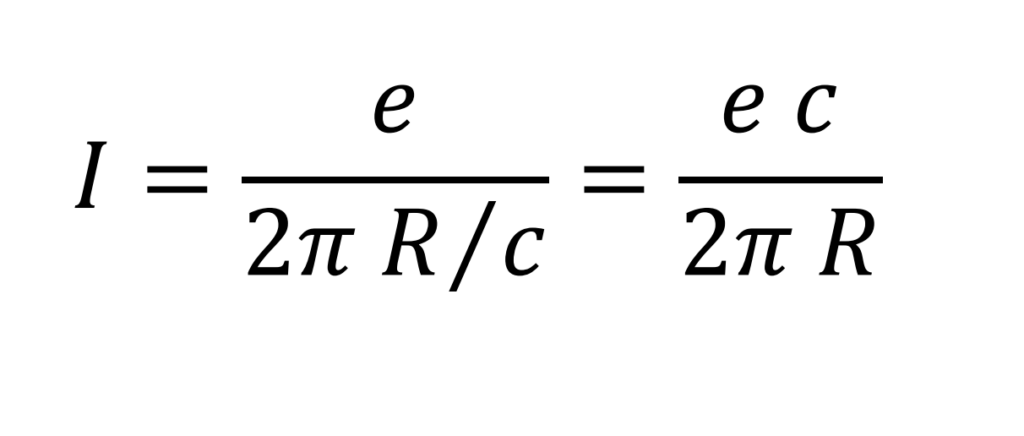
La expresión para el momento magnético
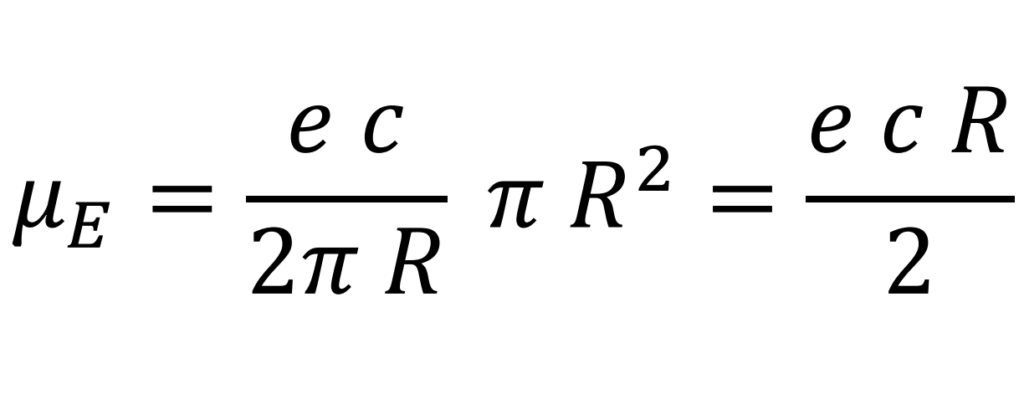
El radio del electrón
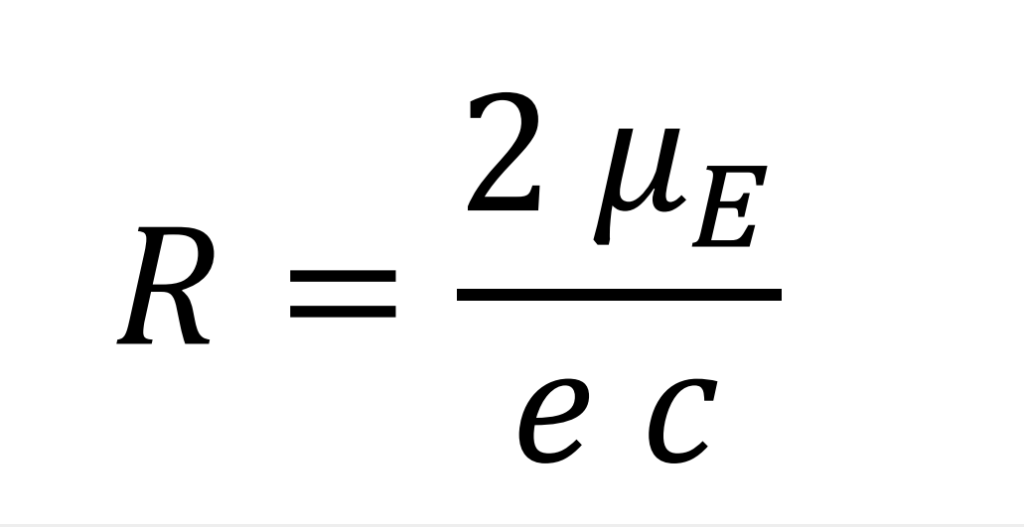
Cálculo del radio crítico del electrón en las condiciones de la formación natural de neutrones en protoestrellas
Para que se inicie la transferencia de carga eléctrica y energía cinética entre el electrón orbital y el protón central, la energía de enlace de cualquier elemento menos su energía potencial eléctrica debe de ser igual a cero.
Expresión general para la energía de enlace en la interacción fuerte (Francisco Ynduráin. Electrones, neutrinos y quarks. La Física de partículas en el siglo XXI 2ª edición CRÍTICA 10.6 p145).
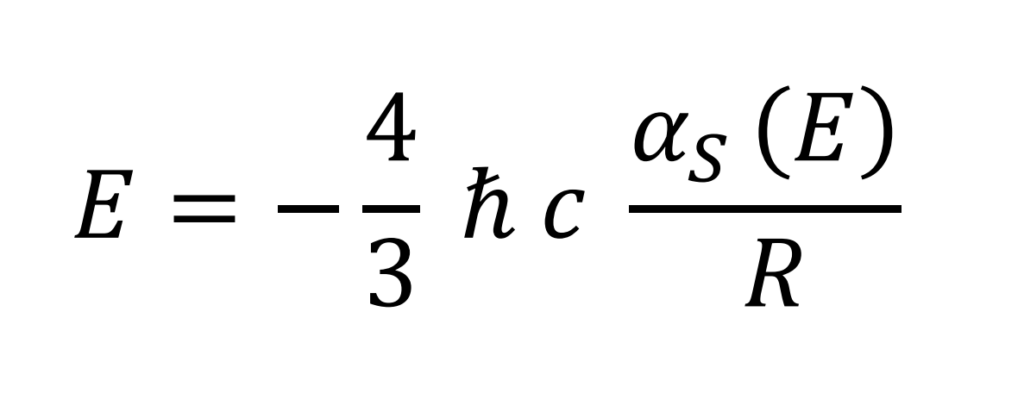
Energía de enlace por elemento (R es el radio del electrón y n el número de elementos)
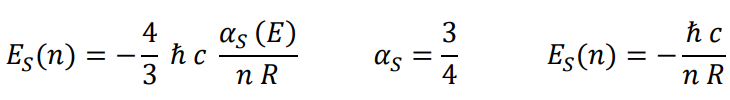
Energía potencial eléctrica por elemento (d es la distancia entre el electrón y el centro de carga del protón)
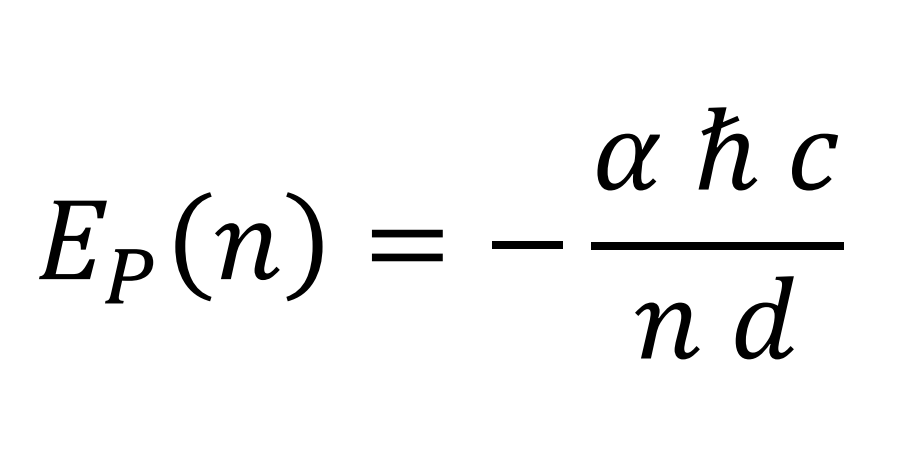
Igualando las dos expresiones
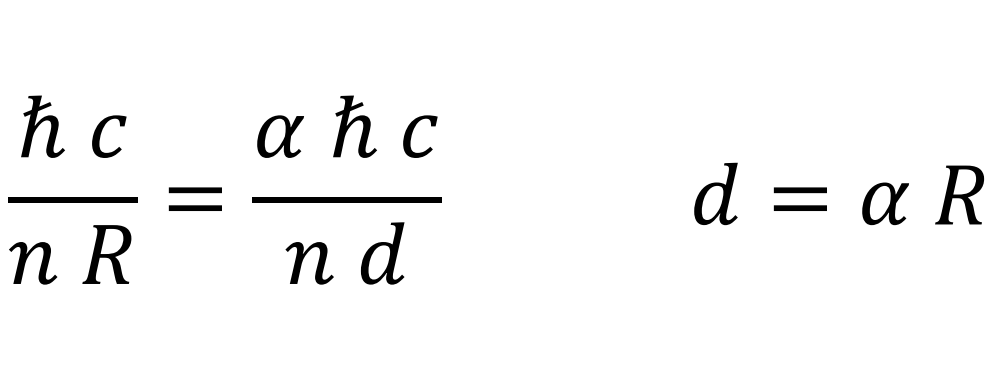
Distancia entre los centros de carga eléctrica del protón y del electrón
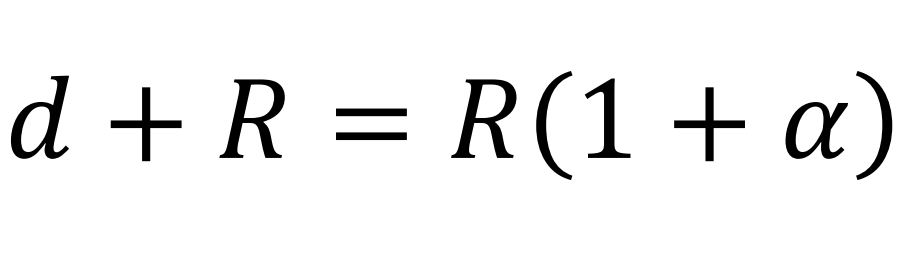
Volumen ocupado por el electrón (empaquetamiento cúbico)
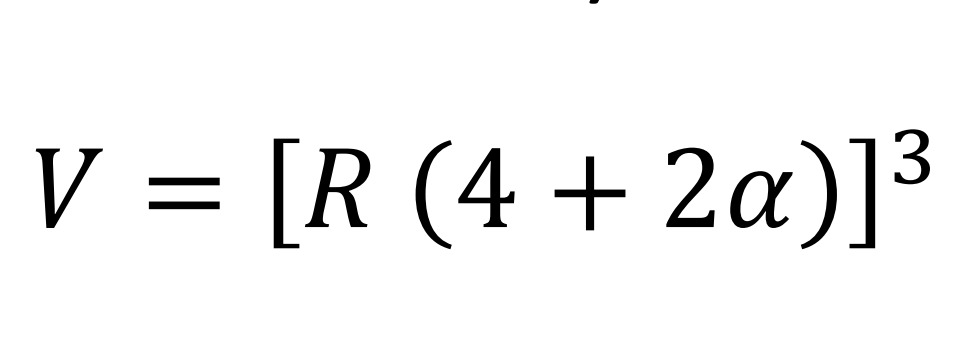
Volumen ocupado por el electrón (empaquetamiento esférico)
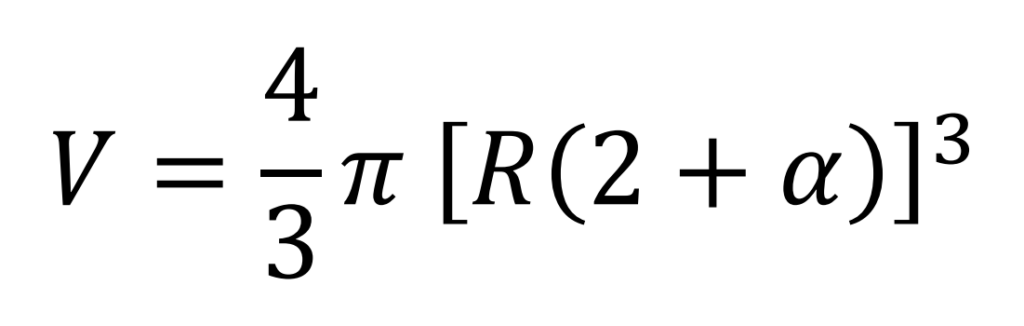
Volumen empírico
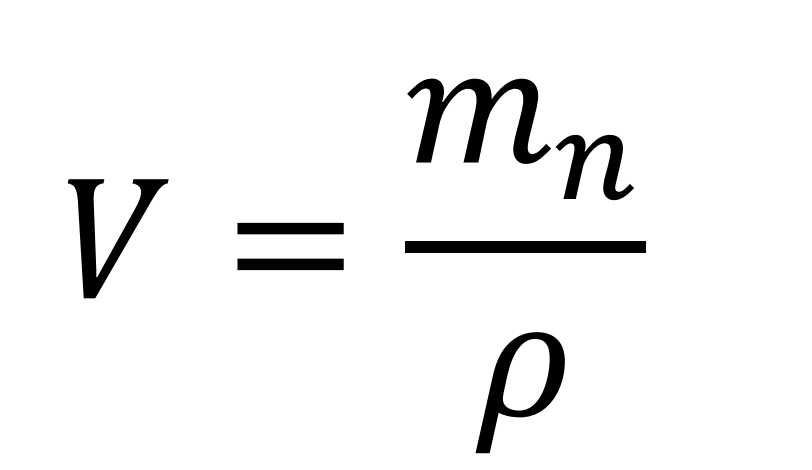
Despejando R (empaquetamiento cúbico)
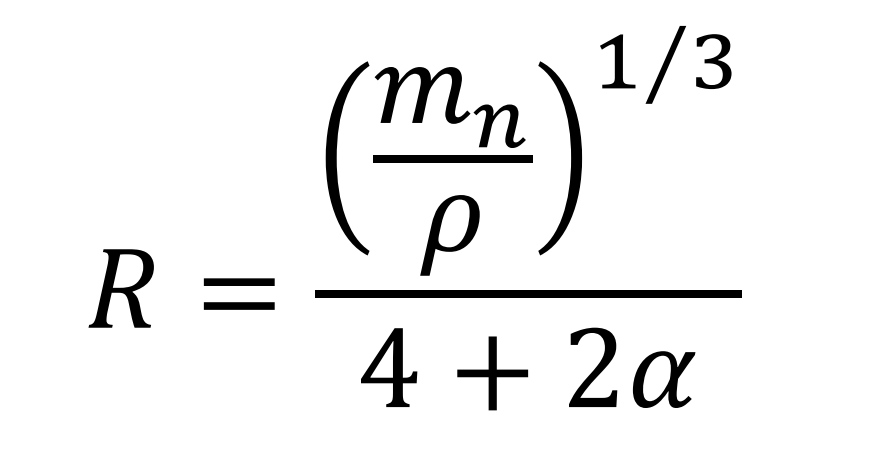
Despejando R (empaquetamiento esférico)
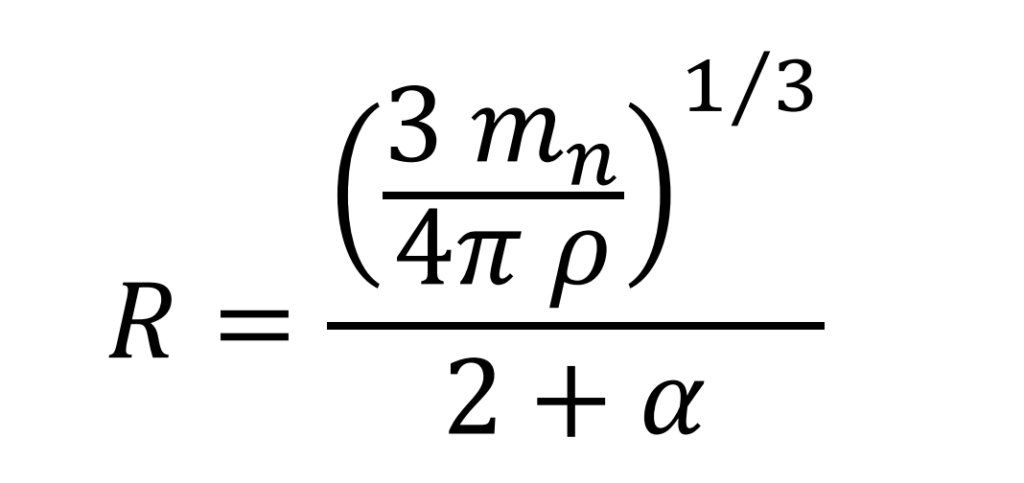
Radio del electrón (valor medio)
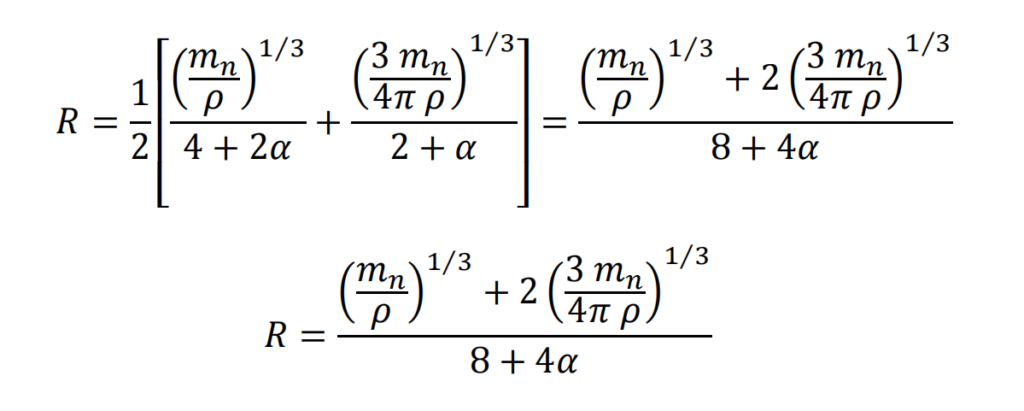
Cálculo de la velocidad lineal de giro
La condición para conseguir la estabilidad del elemento, es que la suma de todas las fuerzas que actúan sobre cualquier porción sea cero. Careciendo de spin, las únicas fuerzas en acción son la electromagnética y la gravitatoria.
El elemento se caracteriza por su simetría radial. Los centros de carga eléctrica y masa coinciden con el centro de simetría. Sus valores son e/n y m/n respectivamente, desplazándose con una velocidad lineal v. La contribución de todos los elementos produce un efecto similar al de una corriente eléctrica continua y circular.
Una porción cualquiera del elemento, con carga eléctrica dq y masa dm, se desplaza con velocidad v atravesando perpendicularmente las líneas del campo magnético.
Se aplica la ecuación de Lorentz, sustituyendo las constantes εo (permitividad eléctrica del vacío) y μo (permeabilidad magnética del vacío). Siendo e la carga eléctrica del electrón y n el número de elementos que lo componen.
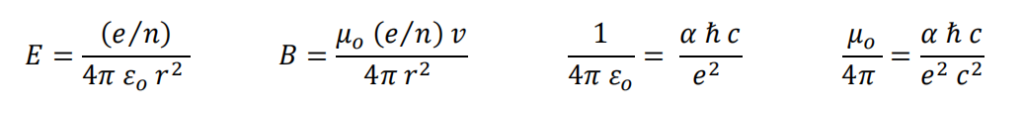
Interacción electromagnética
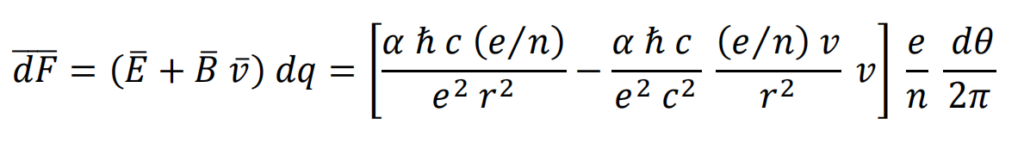
Interacción gravitatoria
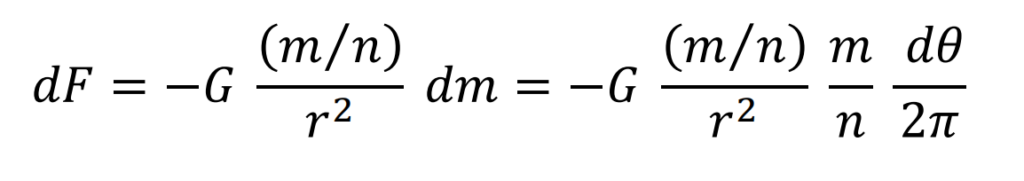
Suma de fuerzas
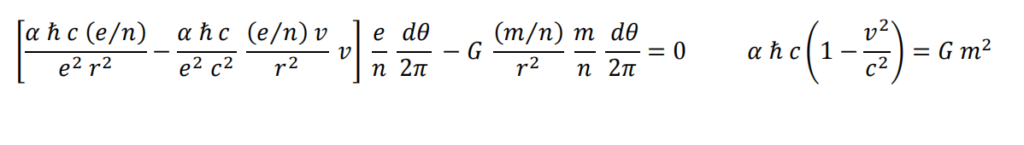
Despejando v
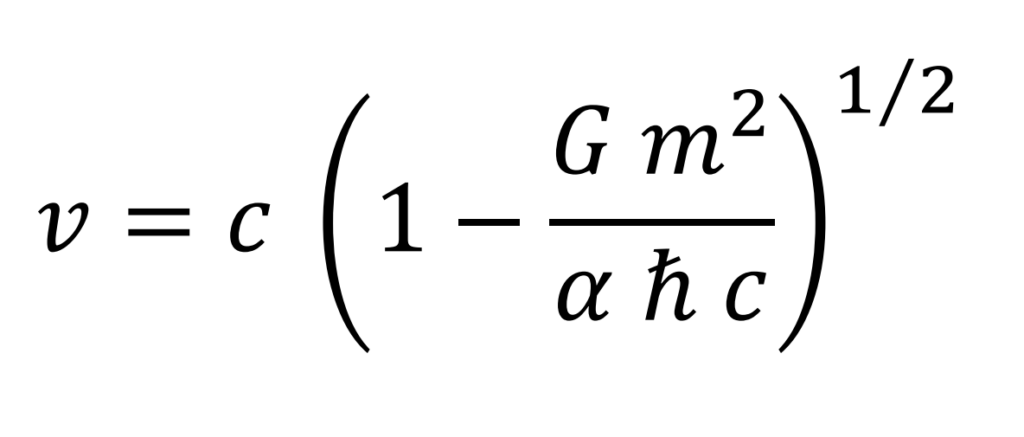
Expresando m en función de mo
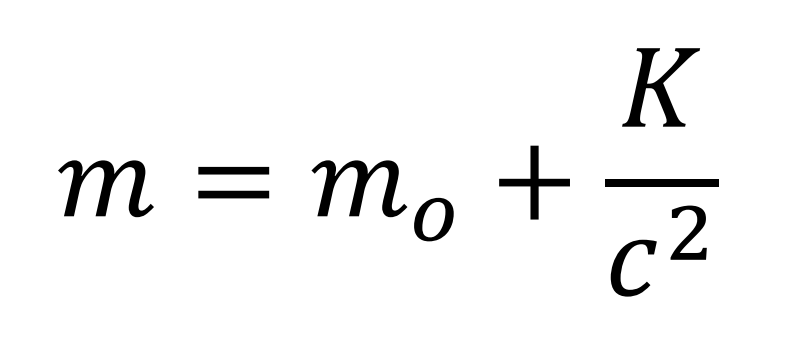
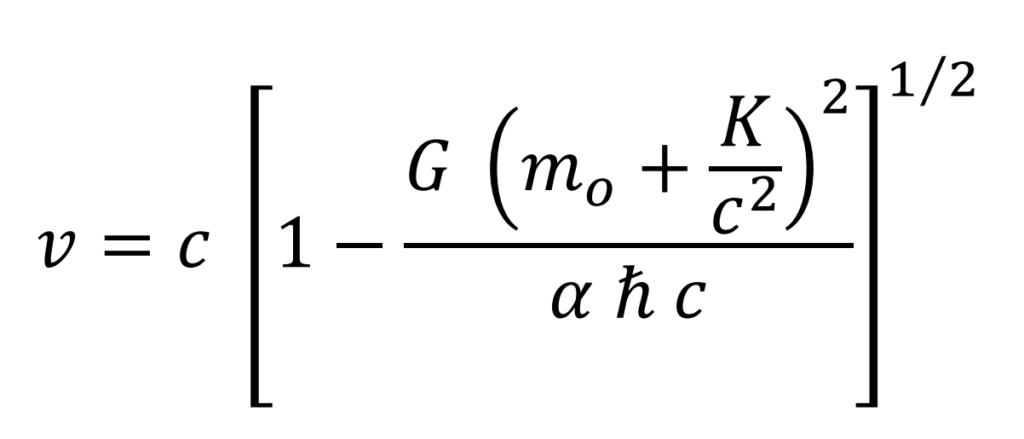
Cálculo del radio de giro
En 1924 Louis Victor de Broglie publicó su tesis doctoral titulada “Investigaciones sobre la teoría cuántica” en la que formulaba la hipótesis de que una partícula material lleva asociada una determinada onda cuya longitud es el cociente entre la constante de Planck y el momento lineal. (Carlos Sánchez del Río. Física Cuántica 5ª Edición PIRÁMIDE 3.3.11)
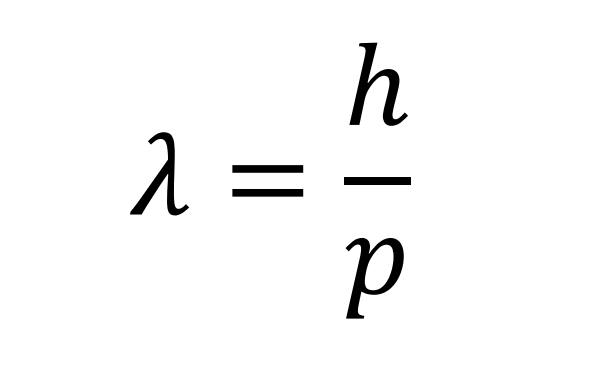
Su hipótesis fue validada experimentalmente en 1929, recibiendo el premio Nobel de Física.
El radio de giro del electrón se considera igual al valor de su longitud de onda asociada expresada en forma reducida.
De esta forma, se cumple la condición de onda estacionaria y no hay pérdidas por radiación en el movimiento de giro.
Situación similar a la órbita del electrón del átomo de hidrógeno para n = 1.
Carlos Sánchez del Río. Física Cuántica 5ª edición PIRÁMIDE 5.4.20
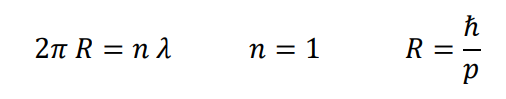
Momento lineal de giro (para un rango muy amplio de energía)
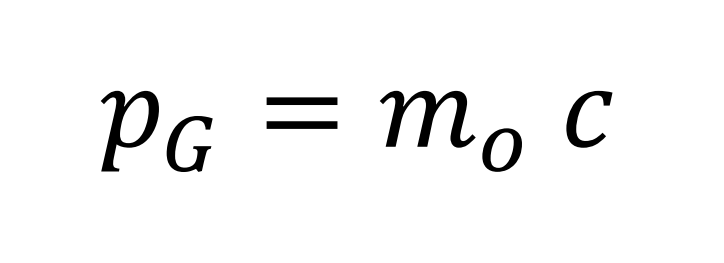
Momento lineal de traslación (Carlos Sánchez del Río. Física Cuántica 5ª Edición PIRÁMIDE 2.4.15)
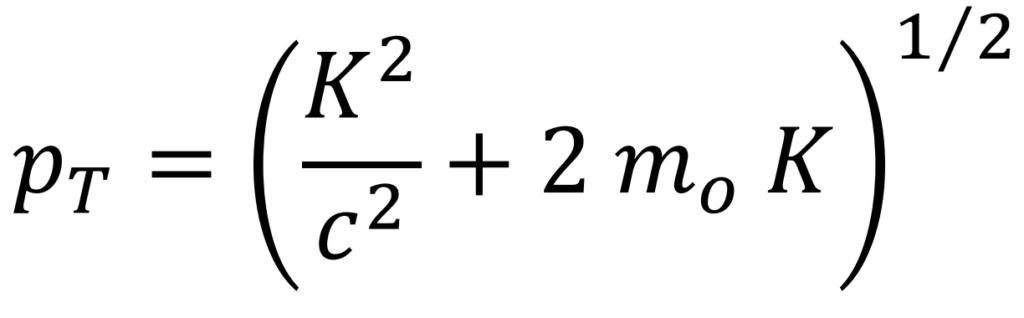
Expresión para el radio de giro
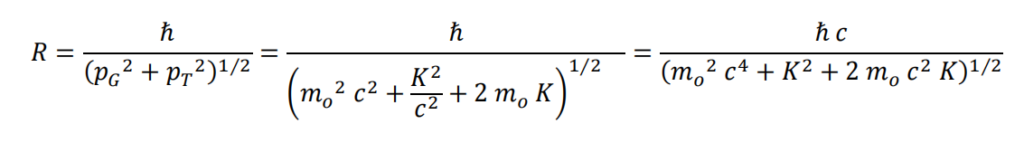
Simplificando
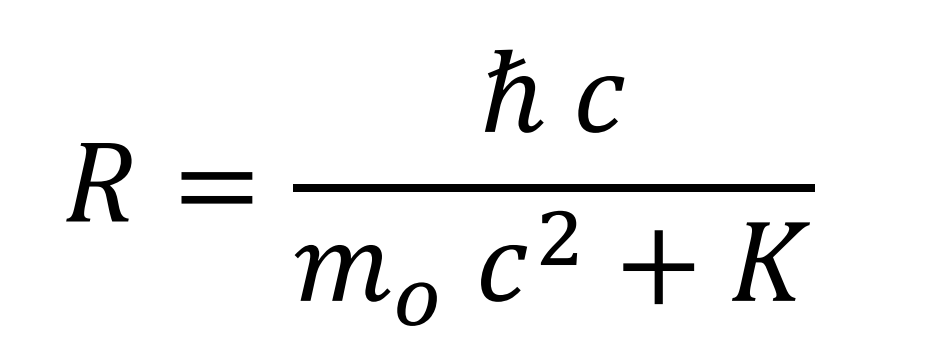
Cálculo del radio del elemento
La velocidad v corresponde a la velocidad lineal del centro de simetría de cualquier elemento. La expresión para la velocidad angular será
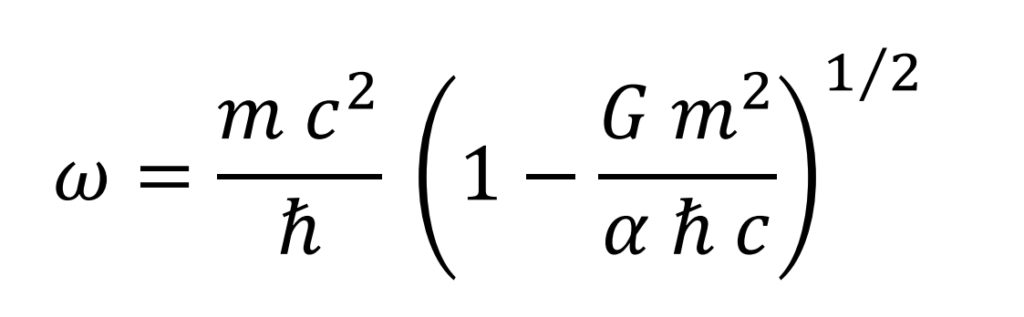
De acuerdo con la teoría de la relatividad especial, la velocidad de propagación de la luz en el vacío c se considera un límite no superable por ningún objeto en movimiento.
Asumiendo que el elemento presenta simetría radial con un determinado radio r, el criterio aplicado para calcularlo será que su velocidad periférica sea infinitesimalmente menor que c en el caso especial del electrón en reposo. En este caso los valores de R y de v son máximos y la masa es mo

Cálculo del número de elementos
El valor de la constante de estructura fina α aumenta con la energía.
Francisco Ynduráin. Electrones, neutrinos y quarks. (La Física de partículas en el siglo XXI 2ª edición CRÍTICA 10.7 p149).
Valores para la constante de estructura fina, α0 = 1/137,036 y α91,2GeV = 1/128,96.
La masa del electrón en función de su velocidad de giro, viene dada por la expresión
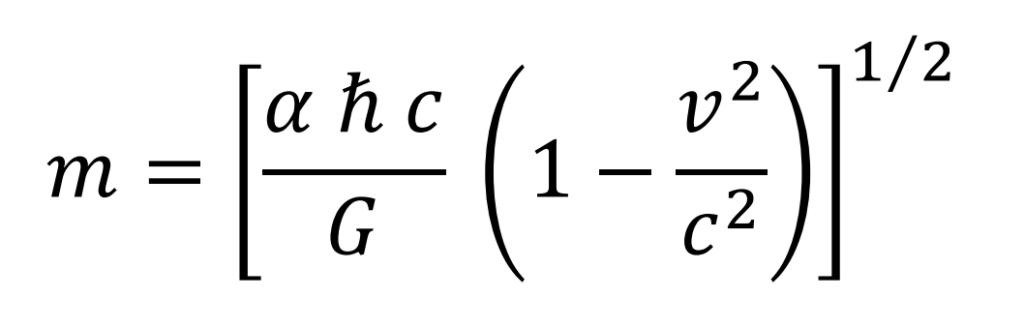
En el caso especial de una velocidad de giro prácticamente nula, se asigna por hipótesis un valor de 1 a la constante de estructura fina α. La expresión para la masa del electrón, coincide con la masa de Planck.
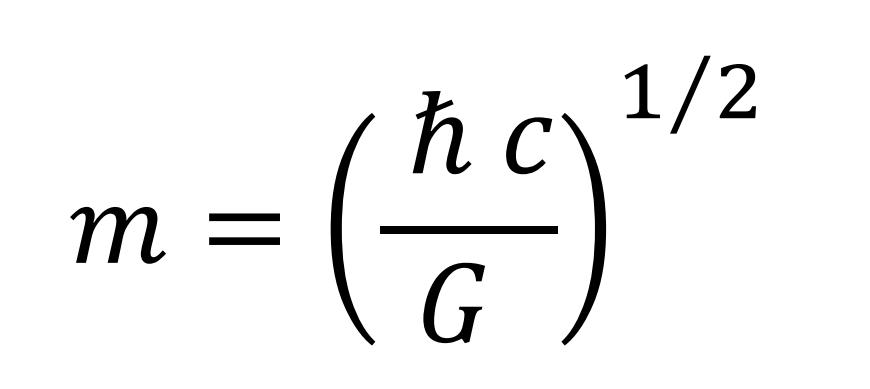
El valor del radio de la órbita para este caso coincide con la longitud de Planck.
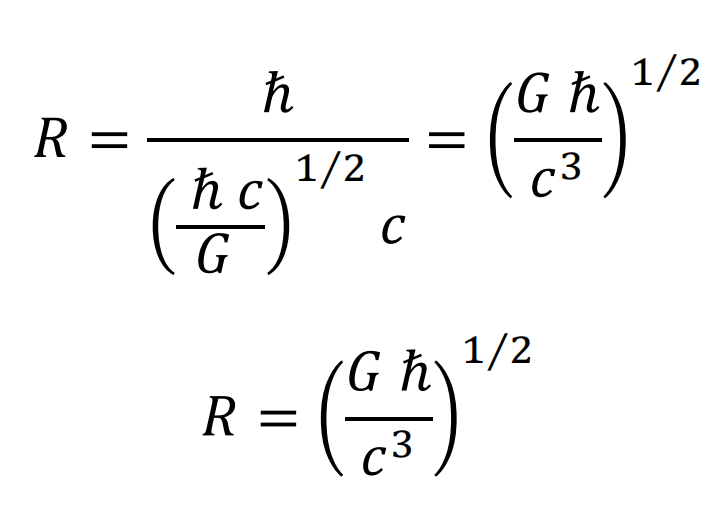
Los elementos se agruparían adyacentes, ocupando en su totalidad la longitud de una circunferencia de radio igual a la longitud de Planck.
El número de elementos es el cociente entre la longitud de la órbita y el diámetro del elemento
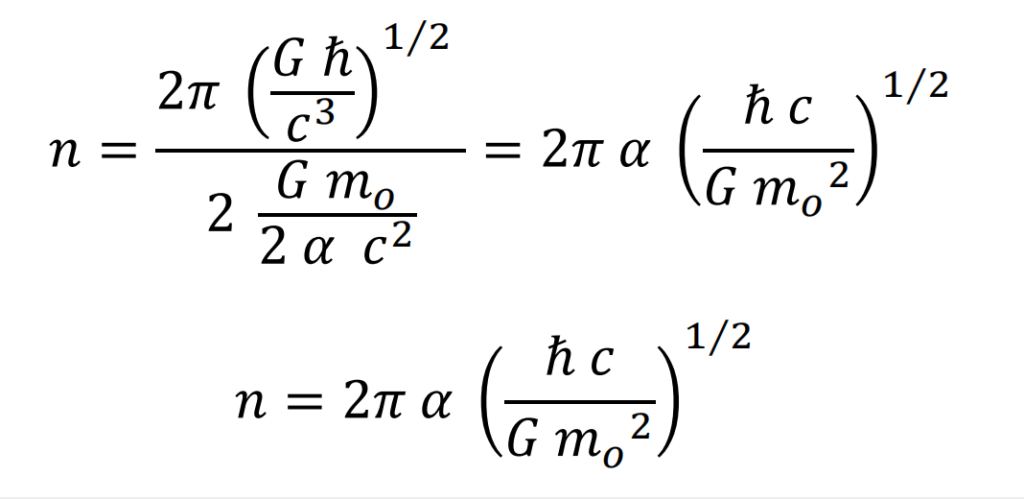
Como curiosidad, el valor de n calculado por la hipótesis coincide prácticamente con la cuarta parte del producto del Número de Avogadro por la Constante de Estructura Fina
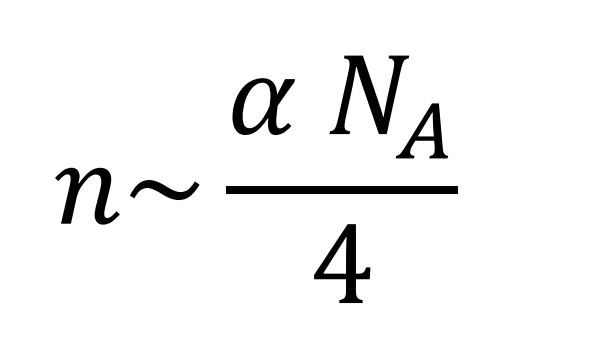
Cálculo para la constante de acoplamiento y expresión para la interacción fuerte
Para que el conjunto permanezca estable la suma de todas las fuerzas que actúan sobre cualquier elemento será nula.
Fuerza de inercia
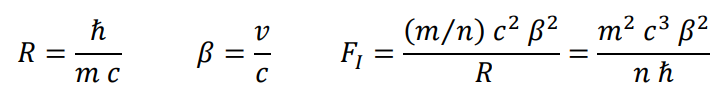
Fuerza eléctrica
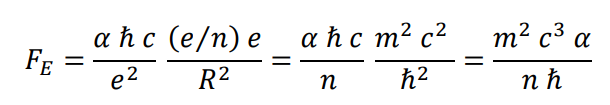
Fuerza gravitatoria
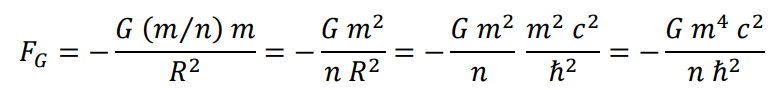
Suma de fuerzas y expresión de la nueva interacción
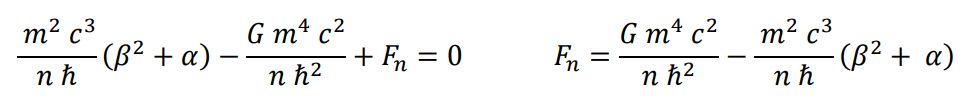
Francisco Ynduráin. Electrones, neutrinos y quarks. (La Física de partículas en el siglo XXI 2ª edición CRÍTICA 10.6 p145).
Expresión para la energía de enlace fuerte
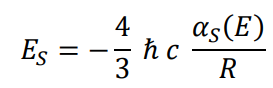
Igualando las dos expresiones para las interacciones y substituyendo R
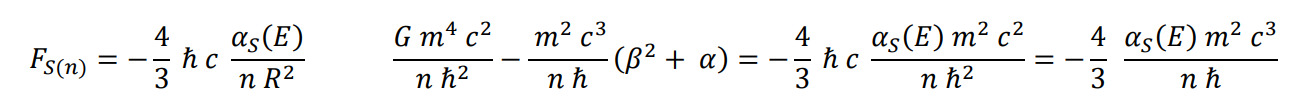
Despejando la incógnita (Expresión para la constante de acoplamiento fuerte)
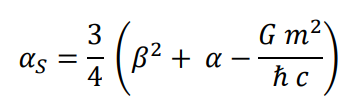
Expresión para la interacción fuerte, se desprecia la interacción gravitatoria
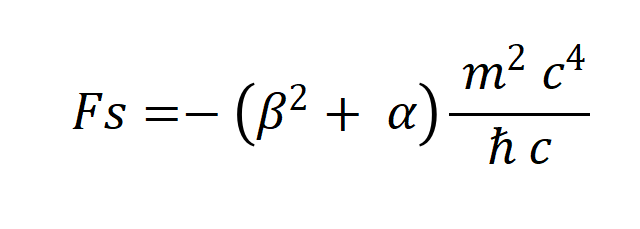
Energía cinética del electrón en las condiciones del experimento de Stern – Gerlach
La energía cinética será similar a la primera energía de ionización del átomo de plata (Ag →Ag+)
E (Ag→Ag+) = 731 kJ/mol = 7,58 eV/átomo
Redondeando K = 8 eV
Energía cinética del electrón en las condiciones iniciales del proceso de formación de neutrones en protoestrellas
La energía cinética corresponde al producto de la diferencia de la masa del neutrón menos las masas del protón y del electrón en reposo, multiplicada por c2
Masa del neutrón por c2 939,565 MeV
Masa del protón por c2 938,272 MeV
Masa en reposo del electrón por c2 0,511 MeV
K = 939,565 – 938,272 – 0,511 = 0,782 MeV
En Bilbao a 15 de octubre de 2024